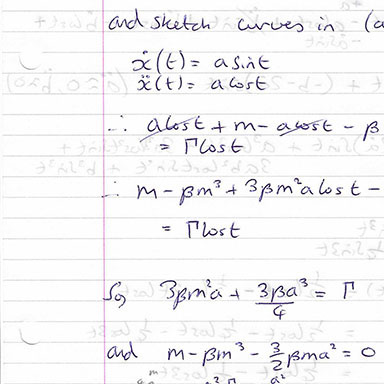Open University - Maths MSc

I studied maths at undergraduate level (quite a long time ago), graduating with a very average BSc (Hons) Mathematics from the University of Warwick.

After a number of years focused on hacking computers, and with a bunch more maturity and interest, I decided to return to study for the MSc Mathematics with the Open University.

The OU offers distance part-time learning to fit around regular life commitments (job, family, etc.) - so I’ve been able to gradually pass modules over the past few years.

The MSc requires 6 modules to complete - so far I’ve completed 4, allowing me to claim a Postgraduate Diploma in Mathematics. My plan is to complete the final 2 within the new few years, as time and energy permit!

The following are the modules that I’ve studied so far:

M820 - Calculus of Variations & Advanced Calculus - 2017/18

M820 was the first module that I studied, and concerns the Calculus of Variations (and a set of relevant tools and technique from calculus). This is designed as an entry module into the course, and so provides a great revision of relevant background maths at the start.

It was a lot of work to re-learn the basics of calculus and differential equations on top of all the new material - but this was a fascinating course covering some important topics from applied maths such as Noether’s Theorem and Sturm-Liouville Theory.

Here’s a sample problem from the coursework:

M821 - Nonlinear Ordinary Differential Equations - 2018/19

M821 was the second module (which I took alongside M823 below), and is presented in a very similar style to M820.

M821 is all about ODEs describing non-linear oscillators, and techniques to recover approximate solutions or infer long-term behaviours - phase portraits, perturbation series, stability, etc. The course closely follows the book Nonlinear Ordinary Differential Equations by Jordan and Smith

This has been my favourite module - I’ve always enjoyed ODEs.

Here’s a sample problem from the coursework:

M823 - Analytic Number Theory I - 2018/19

M823 has been the only pure maths module that I’ve taken, and consequently my least favourite… I have very little love for numbers! :)

Number theory is all about primes, and Analytic Number Theory uses techniques from analysis to understand their distribution over the set of natural numbers. The course closely follows the book Introduction to Analytic Number Theory by Apostol.

Here’s a sample problem from the coursework:

M833 - Advanced Mathematical Methods - 2021/22

M833 is the latest module that I’ve studied, and is similar in style to M820 and M821 - designed by the same person.

M833 covers a selection of topics, and is broadly based around use of the computer package Maple to explore convergence of various approximation techniques including Padé approximants, asymptotic expansions of integrals and eigenvalue problems.

The Maple element was straightforward (as a seasoned coder), but the other topics were all interesting - although a few had cropped up in other courses already (e.g. Sturm-Liouville Theory).

Here’s a sample problem from the coursework:

Future

I will need to study M840 Dissertation in Mathematics and one other ‘M8..’ module to complete the MSc.